Understanding how computers learn the meaning of words through the famous King-Queen-Man-Woman example
Chapter 1: The Intuitive Explanation (For Anyone)#
Imagine you’re organizing a massive library. Instead of putting books on shelves randomly, you want to place similar books near each other. Romance novels go together, science books cluster in another area, and cookbooks have their own section.
Now imagine doing this with every word in the English language. Words that mean similar things should be “close” to each other in some kind of space. But how do you measure the “distance” between words like “happy” and “joyful”?
This is exactly what vector embeddings do - they give every word a mathematical address (coordinates) in a multi-dimensional space, where similar words live close together.
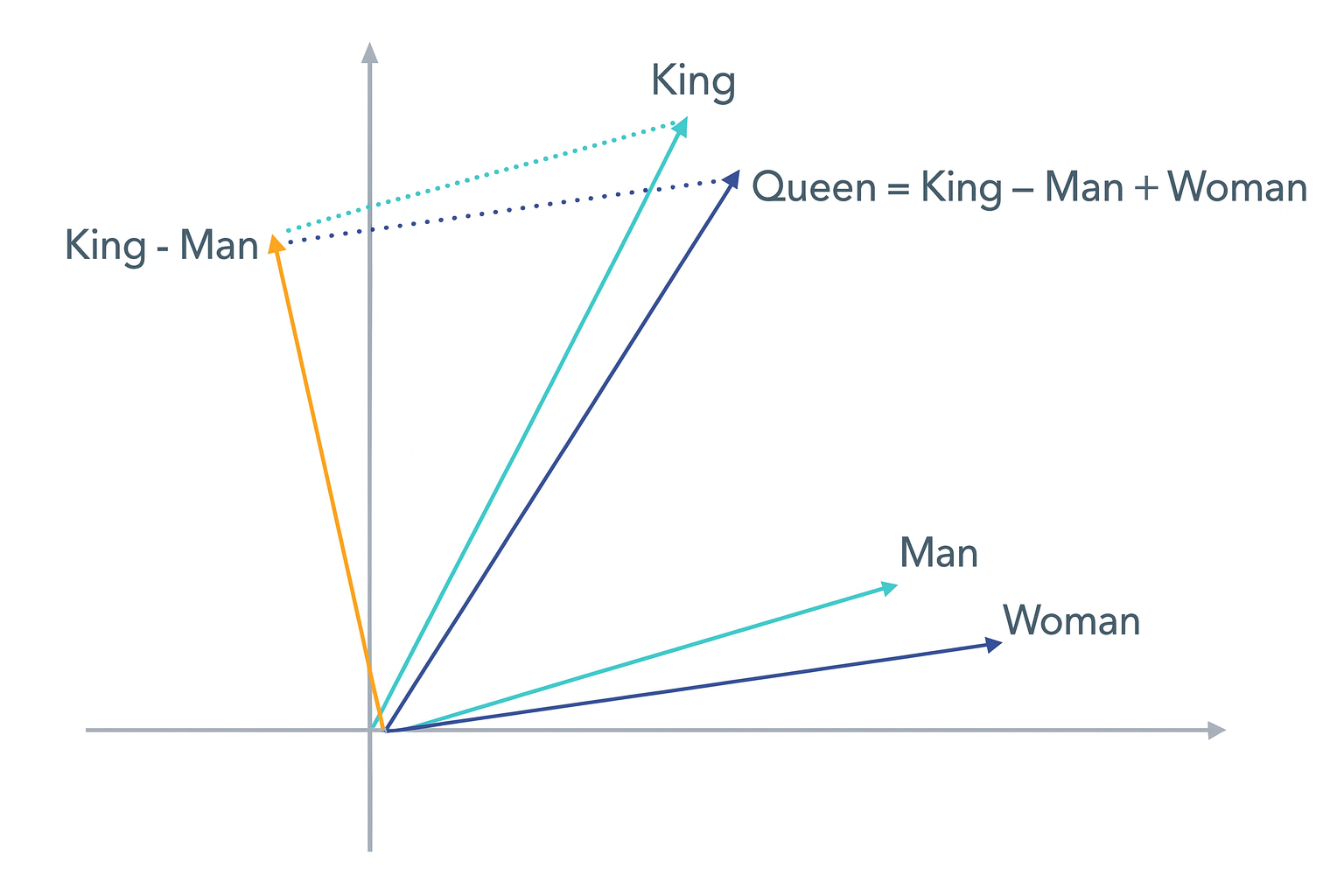
The Magic: When computers learn these addresses correctly, they discover that relationships between words follow mathematical patterns. The relationship between “King” and “Queen” is the same as the relationship between “Man” and “Woman” - it’s just a consistent direction in this word-space.
Chapter 2: The Farmer’s Perspective (Everyday Analogies)#
Let’s say you’re a farmer who knows your land like the back of your hand. You know that:
- Your cornfield is 2 miles east and 3 miles north of your house
- Your neighbor’s cornfield is 1 mile east and 1.5 miles north of your house
- Your barn is 3 miles east and 2 miles north
- Your neighbor’s barn is 2 miles east and 0.5 miles north
Now, here’s something interesting you notice: The direction from your cornfield to your neighbor’s cornfield is exactly the same as the direction from your barn to your neighbor’s barn. Both involve going 1 mile west and 1.5 miles south.
This is the same pattern computers discover with words! The “direction” from King to Queen is the same as from Man to Woman. It’s like discovering that all male-to-female relationships point in the same direction on your farm map.
Your farming wisdom: “If I know where a man lives, I can find where his wife lives by walking in the ‘woman direction.’”
Chapter 3: Setting Up Your Mathematical Laboratory#
Time to prove this with actual measurements! You’ll need:
- Graph paper (1cm squares work well)
- Ruler (for measuring distances)
- Protractor (for measuring angles)
- Colored pens (red, blue, green, black)
Your Coordinate System Setup#
Scale: Each square = 0.5 units
Axes: Draw thick lines for X (horizontal) and Y (vertical)
Range: X from -3 to +5, Y from -2 to +4
Origin: Mark (0,0) with a large dot
4 |
|
3 | • King (2,3)
|
2 | • Man (3,2)
|
1.5 | • Queen (1,1.5)
|
1 |
|
0.5 | • Woman (2,0.5)
0 |----+----+----+----+---- X
0 1 2 3 4 5
-1 |
|
-2 |
Chapter 4: Plotting Our Word Universe#
The Four Words and Their Coordinates#
| Word | X-coordinate | Y-coordinate | What This Means |
|---|---|---|---|
| King | 2.0 | 3.0 | Male + Royal |
| Queen | 1.0 | 1.5 | Female + Royal |
| Man | 3.0 | 2.0 | Male + Common |
| Woman | 2.0 | 0.5 | Female + Common |
Step-by-Step Plotting#
Plot King (2, 3):
- Start at origin (0,0)
- Move 4 squares right (2.0 ÷ 0.5 = 4)
- Move 6 squares up (3.0 ÷ 0.5 = 6)
- Mark with a blue dot and label “King”
Plot Queen (1, 1.5):
- Start at origin
- Move 2 squares right
- Move 3 squares up
- Mark with a red dot and label “Queen”
Plot Man (3, 2):
- Start at origin
- Move 6 squares right
- Move 4 squares up
- Mark with a green dot and label “Man”
Plot Woman (2, 0.5):
- Start at origin
- Move 4 squares right
- Move 1 square up
- Mark with a purple dot and label “Woman”
Drawing the Vectors#
Draw arrows from origin (0,0) to each point using matching colors. These arrows represent the “meaning” of each word in our mathematical space.
Chapter 5: The Mathematical Discovery#
Now for the exciting part - let’s prove that King - Man + Woman = Queen using actual calculations!
Step 1: Calculate King - Man#
King vector: (2, 3)
Man vector: (3, 2)
King - Man = (2-3, 3-2) = (-1, 1)
What does this mean? This vector (-1, 1) represents “the difference between being royal vs. common while staying male.”
Step 2: Add Woman#
King - Man: (-1, 1)
Woman vector: (2, 0.5)
(King - Man) + Woman = (-1+2, 1+0.5) = (1, 1.5)
Step 3: Compare with Queen#
Our calculation result: (1, 1.5)
Actual Queen coordinates: (1, 1.5)
Perfect match! ✓
Chapter 6: Physical Verification with Measurements#
Measuring the “Gender Transformation”#
Draw two arrows on your graph:
Arrow 1 (Red): Man → Woman
- Start: Man (3, 2)
- End: Woman (2, 0.5)
- Vector: (-1, -1.5)
Arrow 2 (Blue): King → Queen
- Start: King (2, 3)
- End: Queen (1, 1.5)
- Vector: (-1, -1.5)
Physical Measurements#
Using your ruler:
- Length of red arrow: √[(-1)² + (-1.5)²] = √[1 + 2.25] = √3.25 ≈ 1.8 units
- Length of blue arrow: √[(-1)² + (-1.5)²] = √[1 + 2.25] = √3.25 ≈ 1.8 units
Convert to paper measurements: 1.8 units × 2 squares/unit = 3.6 squares ≈ 3.6 cm
Using your protractor: Both arrows should point in the same direction. The angle from horizontal:
- Slope = -1.5/-1 = 1.5
- Angle = arctan(1.5) ≈ 56.3° below the negative X-axis
What You Should Observe#
Both arrows are identical - same length, same direction, just starting from different points. This proves that the “gender transformation” is consistent whether you’re talking about royalty or commoners.
Chapter 7: Understanding Similarity Through Dot Products#
Now let’s explore how computers measure word similarity using the dot product.
The Dot Product Formula#
For two vectors A = (a₁, a₂) and B = (b₁, b₂): A · B = a₁ × b₁ + a₂ × b₂
Calculating Similarities#
King · Queen: (2, 3) · (1, 1.5) = (2 × 1) + (3 × 1.5) = 2 + 4.5 = 6.5
King · Man: (2, 3) · (3, 2) = (2 × 3) + (3 × 2) = 6 + 6 = 12
King · Woman: (2, 3) · (2, 0.5) = (2 × 2) + (3 × 0.5) = 4 + 1.5 = 5.5
Man · Woman: (3, 2) · (2, 0.5) = (3 × 2) + (2 × 0.5) = 6 + 1 = 7
Queen · Woman: (1, 1.5) · (2, 0.5) = (1 × 2) + (1.5 × 0.5) = 2 + 0.75 = 2.75
Interpreting the Results#
Higher dot product = more similar words:
- King ↔ Man: 12 (both male, highest similarity)
- Man ↔ Woman: 7 (both common people)
- King ↔ Queen: 6.5 (both royal)
- King ↔ Woman: 5.5 (least related)
- Queen ↔ Woman: 2.75 (both female, but different social status)
This matches our intuition! Kings are most similar to men, then to queens, and least similar to women.
Chapter 8: Cosine Similarity (The Professional Measure)#
Dot products depend on vector length. For fair comparison, we use cosine similarity:
cosine_similarity(A, B) = (A · B) / (|A| × |B|)
Calculate Vector Magnitudes#
|King| = √(2² + 3²) = √13 ≈ 3.61 |Queen| = √(1² + 1.5²) = √3.25 ≈ 1.80 |Man| = √(3² + 2²) = √13 ≈ 3.61 |Woman| = √(2² + 0.5²) = √4.25 ≈ 2.06
Cosine Similarities#
King ↔ Queen: 6.5 / (3.61 × 1.80) ≈ 1.00 (perfectly aligned!) King ↔ Man: 12 / (3.61 × 3.61) ≈ 0.92 Man ↔ Woman: 7 / (3.61 × 2.06) ≈ 0.94
Values close to 1.0 mean very similar directions in our word space.
Chapter 9: Finding Similar Words (Nearest Neighbors)#
Imagine you want to find words similar to “King.” You’d calculate the cosine similarity between King and every other word, then pick the closest ones.
Example: What’s most similar to King?#
Based on our calculations:
- Queen (1.00) - Makes sense! Both royal
- Man (0.92) - Makes sense! Both male
In real word embeddings with thousands of words, “King” might be most similar to: Emperor, Monarch, Prince, Ruler, etc.
Chapter 10: The Big Picture - Why This Matters#
What You’ve Just Learned#
- Words become numbers that computers can manipulate
- Meaning becomes geometry - similar words cluster together
- Relationships become directions - analogies are vector arithmetic
- Similarity becomes measurable - we can quantify how alike two concepts are
Real-World Applications#
Search Engines: When you search for “car,” results for “automobile” and “vehicle” appear because they’re close in embedding space.
Translation: “Hola” (Spanish) and “Hello” (English) have similar embeddings, even though they’re different languages.
Recommendation Systems: If you like “Shakespeare,” you might also like “Hemingway” because they’re nearby in author-space.
Chatbots: AI understands that “How are you?” and “How’s it going?” mean the same thing because they have similar embeddings.
The Power of High Dimensions#
Our example used only 2 dimensions, but real embeddings use 300-1000+ dimensions. This allows them to capture incredibly subtle relationships:
- “France” is to “Paris” as “Italy” is to “Rome”
- “Swimming” is to “Water” as “Flying” is to “Air”
- “Doctor” is to “Hospital” as “Teacher” is to “School”
Chapter 11: Teaching This to Your Students#
Progressive Learning Path#
Level 1: Intuition (5 minutes)
- Library organization analogy
- Similar things should be close together
Level 2: Visualization (15 minutes)
- Plot the four words on graph paper
- Show that they form meaningful clusters
Level 3: Basic Math (20 minutes)
- Calculate King - Man + Woman = Queen
- Verify with actual coordinates
Level 4: Measurements (15 minutes)
- Use ruler and protractor to verify relationships
- Measure that gender transformations are parallel
Level 5: Similarity (20 minutes)
- Introduce dot products
- Calculate and interpret similarity scores
Level 6: Applications (10 minutes)
- Connect to search engines, translation, AI
Common Student Questions#
Q: “Why don’t we just use a dictionary?” A: Dictionaries tell us definitions, but embeddings tell us relationships. They capture that “King” and “Monarch” are similar in ways a dictionary can’t quantify.
Q: “How does the computer learn these coordinates?” A: By reading millions of sentences and noticing which words appear together. Words that show up in similar contexts get similar coordinates.
Q: “Why does the math work so perfectly?” A: Because language has consistent patterns! If you can be male or female, and royal or common, these become independent “directions” in meaning-space.
Conclusion: From Farmer’s Wisdom to AI Magic#
You started with a simple intuition about organizing similar things together, worked through the farmer’s analogy about consistent directions on a map, and ended up measuring mathematical relationships with a ruler and protractor.
This journey from intuition to mathematics is exactly how vector embeddings work - they capture our human understanding of language relationships and make them computable. The same principles that let you navigate your farm let computers navigate the landscape of human meaning.
The fundamental insight: Meaning has geometry, and geometry has math, and math has power.
Now you understand why the simple equation King - Man + Woman = Queen represents one of the most beautiful discoveries in artificial intelligence - that human language follows mathematical laws that computers can learn and use.

